Square and triangular numbers

Akmalova Nargiza student of Tashkent State Pedagogical University named after Nizami

Annotation: This article is about square and triangular numbers and their properties. You can get useful information about square and triangular numbers through the article.

Keywords: square, triangle, square numbers, triangular numbers, number, math.

          Numbers may vary. In school lessons, operations are mainly performed on natural numbers, fractional numbers, whole numbers, rational numbers, irrational numbers and real numbers. At the same time, students may have a question: “What other numbers are there in mathematics?”. Of course, there are many types of numbers in the world of mathematics. One such interesting number is the square number.

           Square numbers. Almost everyone knows the shape of a square. A square is a rectangle with equal opposite sides or a rhombus with right angles. (Figure 1). Square numbers, like their name, are numbers that can be placed in the form of a square (Figure 2).

                                                      

Everyone knows how to calculate the square of a given number, especially if it is not too large. 2 ² = 4, 3 ² = 9, 4 ² = 16 and so on. The answer to the question why the act of multiplying a number by itself is called a square is related to square numbers.

Triangle numbers. Triangular numbers owe their name to a similar construction, now of triangles. Actually we already used triangular numbers in the proof of Lemma 3 above. Triangular numbers are in the form 1, 3, 6, 10, 15, … The general formula is that for every n the number N = n(n+1)/2 is triangular and describes the number of points arranged in a triangular shape with n points on a side as shown below. Where n is the number of crosses on the side of the triangle.here n is the number of crosses on the side of the triangle. (Figure 3)

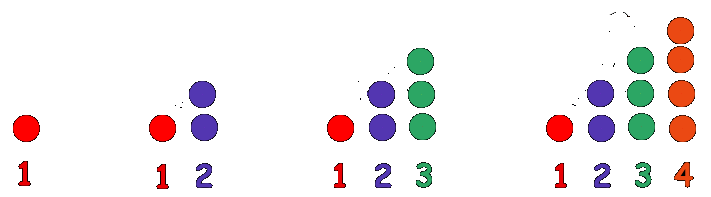
Properties of triangular numbers:

1.Half of the third triangular number n of the sequence of triangular numbers n is multiplied by n + 1:

2.The sum of the previous triangular number and the nth triangular number, i.e. equal to (n-1)-th n squared:         

3. The difference of n-triangle minus one minus n-triangle is equal to n:

4.The sum of the first n triangular numbers is called the tetrahedral number Sn and is equal to one sixth of the product of n multiplied by (n + 1) and multiplied by     (n + 2):

S _n 

5.Every natural number is the result of the sum of three triangular numbers:

References:

1.    What is a number?, Site link:  http://www.cut-the-knot.org/do_you_know/numbers.shtml#square

• https://www.cut-the-knot.org/do_you_know/diffDist.shtml
• https://www.isallaboutmath.com/triangnum1.aspx (an online and iPod video by Julio de la Yncera)