Systems of Linear Equations and Solving Them Using Cramer’s Rule

Kokand State University    

Faculty of Exact Sciences and Digital Technologies   

Student: Mamadaliyeva Durdona  

E-mail:durdonamamadaliyeva60@gmail.com                                                        

Abstract: In this scientific article, the theoretical foundations and practical application of solving systems of linear equations using Cramer’s rule are described. The method is based on determining the unknowns through determinants and is applicable only when the main determinant is nonzero. The algorithm steps are demonstrated on examples with two and three unknowns, and the general form of the formulas is presented.

Keywords: Cramer’s rule, trapezoid, system of linear equations, algebraic method, determinant, constant term.

Аннотация: В данной научной статье раскрываются теоретические основы и практическое применение решения систем линейных уравнений методом Крамера. Метод основан на определении неизвестных с помощью определителей и применяется только в случаях, когда главный определитель не равен нулю. На примерах с двумя и тремя неизвестными показаны этапы алгоритма и приведена общая форма формул.

Ключевые слова: метод Крамера, трапеция, система линейных уравнений, алгебраический метод, определитель, свободный член.

Systems of linear equations arise in many fields of science, engineering, and economics. Solving such systems efficiently and accurately is an important skill in linear algebra. One of the classical methods for solving systems with a unique solution is Cramer’s Rule, which is based on the concept of determinants.

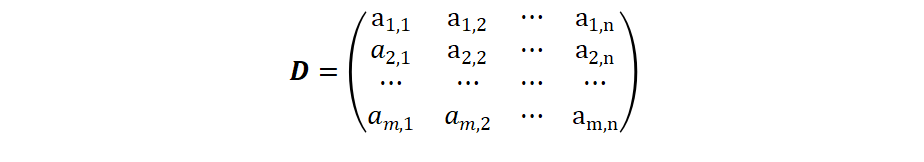
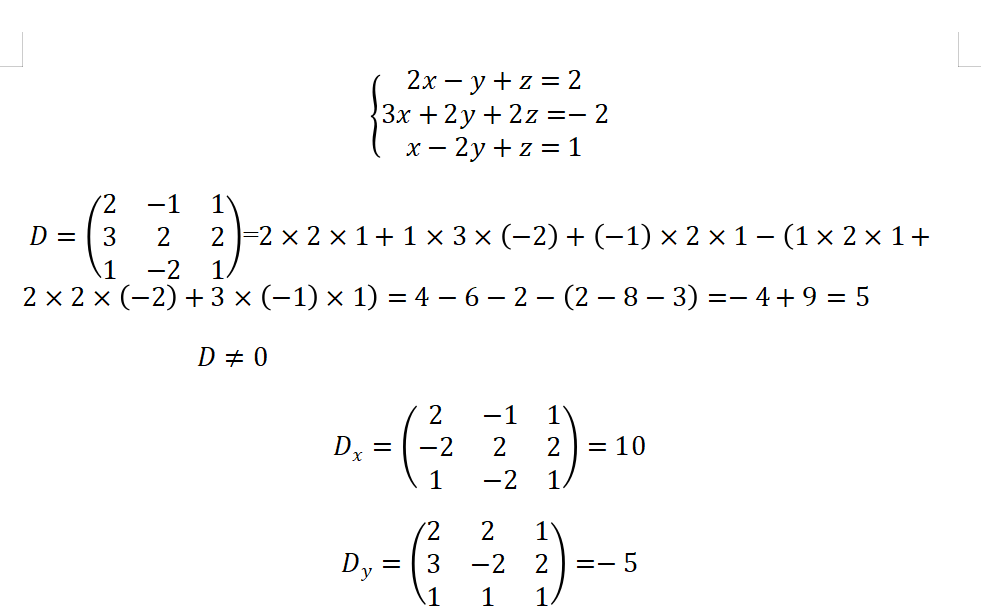
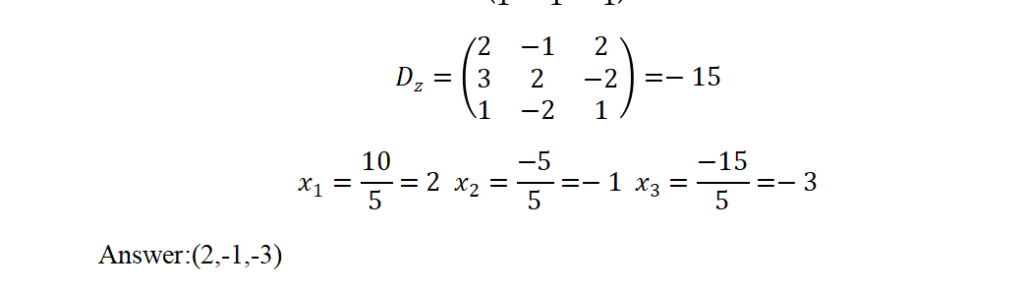
For systems with a non-zero determinant, Cramer’s rule is one of the simplest and most convenient methods to understand and apply.

                                     References:

·  Azlarov, T., & Mansurov, Kh. (1994). Mathematical Analysis, Vol. 1. Tashkent: “O‘qituvchi”. 315 pages.

·  Azlarov, T., & Mansurov, Kh. (1995). Mathematical Analysis, Vol. 2. Tashkent: “O‘qituvchi”. 336 pages.

·  Ayupov, Sh. A., & Berdikulov, M. A. (2004). Theory of Functions. Tashkent: “O‘AJBNT” Center. 148 pages.

·  Turgunbayev, R. (2008). Mathematical Analysis, Part 2. Tashkent: TDPU.

·  Jo‘rayev, T., et al. (1999). Fundamentals of Higher Mathematics, 2nd ed. Tashkent: “O‘zbekiston”.